Ресемплинг аудио.

В этом посте расскажу о ресемплинге аудио (в частности, о даунсемплинге), под чем я подразумеваю понижение частоты дискретизации, с которой был записан звук. Известно, что в компьютере непрерывный аудио сигнал представлен в виде семплов (по-русски, измерений), сделанных в равно отстоящие друг от друга промежутки времени. Например, если звук записан с частотой дискретизации 44.1 кГц, то за одну секунду было сделано 44100 семплов. Здесь я расскажу о том, как восстановить исходный непрерывный сигнал по взятым семплам и как выбирать и менять частоту семплирования (или, что то же самое, частоту дискретизации).

Преобразование Фурье.

Преобразованим Фурье $F(\xi)$ функции $f(x)$ называется следующая функция:

$F(\xi) = \int_{-\infty}^{\infty} f(x) e^{-ix\xi}dx$

обратное преобразование определено как

$f(x) = \frac{1}{2\pi}\int_{-\infty}^{\infty} F(\xi) e^{ix\xi}d\xi$

Вопрос о том, когда существует преобразование Фурье и обратимо ли оно (т.е. работает ли вторая формула), очень сложен, и я коснусь его здесь лишь частично. Пока я скажу только, что если обратное преобразование существует, то $\lim_{Re \xi \to \infty} F(\xi) = 0$ при некоем $Im(\xi) = const$. Преобразование Фурье (и схожее преобразование Лапласа, в котором отсутствует никому не нужная $i$ :) используется в разных областях сельского хозяйства. Например, с помощью преобразования Лапласа особенно легко решать некоторые ODE и PDE. Но я пишу про него потому, что с помощью него можно получить фазовые и частотные характеристики сигнала. Множитель $exp (ix\xi)$, с которым мы интегрируем функцию-оригинал можно представить в виде $cos(\xi x) + i sin (\xi x)$, т.е. как гармоничный осциллятор с частотой $\xi$. Если мы возьмем модуль функции $F(\xi)$, то узнаем, какие частоты есть в нашем сигнале.

У преобразования Фурье есть ряд важных свойств, из которых я приведу 3:

1. Линейное свойство: $F[af(x) + bg(x)] = aFf(x) + bFg(x)$ (здесь и далее запись $Ff(x)$ значит "применить преобразование Фурье к функции $f$".
2. Свойство сдвига: $Ff(x-a) = e^{ia\xi}Ff(x)$.
3. Произведение изображений: $F[f*g(x)] = Ff(x)Fg(x)$.

Обозначение $f*g(x)$ выше означает свертку, т.е. 

$f*g(x) = \int_{-\infty}^{\infty} f(\tau) g(x-\tau) d\tau$

Или, если функции равны нулю при $x<0$:

$f*g(x) = \int_{0}^{x} f(\tau) g(x-\tau) d\tau$

Сигнал, ограниченный по частоте.

Представим сигнал, частотная составляющая которого равна $F(\xi) = 1$ при $\left|\xi\right| < \omega_{0}$ и $ F(\xi) = 0$ иначе.

Обратное преобразование Фурье этого сигнала равно $f(x) = \frac{1}{2\pi}\int_{-\omega_{0}}^{\omega_{0}}exp(ix\xi)d\xi = \frac {sin(\omega_{0}x)}{\pi x}$.

Существует так называемая Shannon sampling theorem (в переводе — "теорема Котельникова", и, если верить русской википедии, первенство принадлежит именно русскому ученому), которая гласит, что любой сигнал, ограниченный по частоте (т.е., имеющий частоты $f < f_{0} = \frac{\omega_{0}}{2\pi}$), можно в точности реконструировать из семплов, взятых с частотой $2f_{0}$. Этот сигнал представим в виде суммы функций $\frac{sin(\omega x)}{\pi x}$, отмасштабированных и сдвинутых по времени на значения $\frac{2\pi n}{\omega_{0}}$, где $n$ - натуральное число.

 Теперь, что будет, если для представления в компьютере гармонического сигнала частотой 2 кГц выбрать частоту дискретизации меньше 4 кГц? Всё просто — точная реконструкция сигнала будет невозможна, так как неправильно взятые семплы будут "интерпретированы" как сигнал меньшей частоты, чем есть на самом деле.

Если мы видим файл с частотой дискретизации 96 кГц, то сразу понимаем, что он может нести информацию о сигнале, ограниченном по частоте до 48 кГц, то есть далеко за пределами возможности восприятия человека (взрослый человек слышит максимум до 16-17 кГц, а ребенок — до 20 кГц). Не исключая, что у столь высокой частоты дискретизации есть свои специфические плюсы, я (и не только я) считаю, что файлы с такой частотой — это глупый расход места на диске. Однако, если просто взять и выкинуть каждый второй (скажем, четный) семпл, часть сигнала с частотами, большими, чем новая частота дискретизации/2, будет искажена и перейдет в слышимую часть спектра в виде артефактов. Поэтому перед непосредственно даунсемплингом нужно делать фильтрацию, убирая частоты, которые невозможно представить при новой частоте дискретизации.

Фильтрация сигнала.

Как нам отфильтровать сигнал, чтобы он содержал только нижние частоты? Очевидно, его Фурье-образ нужно умножить на функцию, ограниченную по спектру, такую, как мы рассматривали раньше. Из свойства умножения образов преобразования Фурье (свойство 3) получаем, что это эквивалентно свертке сигнала с функцией вида $\frac{sin(\omega x)}{\pi x}$ Однако, с этим планом возникают проблемы: чтобы получить один семпл фильтрованного сигнала, нам нужно взять все семплы оригинала. Таким образом, сложность фильтрации составляет $O(n^2)$. Куда легче дело обстоит с фильтрами, которые имеют компактный носитель (здесь это эквивалентно тому, что ядро фильтра не равно нулю только на некоторой ограниченной области). Такие фильтры, к сожалению не имеют ограниченного спектра, но могут быть очень-очень близки к идеальному.

Да, в нашем дискретном компьютерном мире "непрерывная" свертка заменяется дискретной, для $f = \phi * \psi$

$f_{n} = \sum_{i=-\infty}^{\infty} \phi_{i} \psi_{n-i}$

На практике, бесконечность в сумме заменяется конечным натуральным $l$, который, вроде бы, называется порядком фильтра.

А что с функциями, у которых нет (обратного) преобразования?

Возьмем $F(\xi)=1$. Она не затухает при $Re \xi \to \infty$, значит у неё нет обратного преобразования, так? Так, да не так. Для осознания этого факта, нужно ввести понятие слабой сходимости в Гильбертовом пространстве. Пусть $f_{n}$ из $H$ сходится к $f$ слабо (обозначается $f_{n} \to^{w} f$), если для любой $\phi \in H$ выполняется $lim_{n \to \infty} \left< f_{n}, \phi \right> = \left< f, \phi \right>$

Возьмем $f_{n} = \frac {sin (n x)}{\pi x}$. Все эти функции принадлежат к $L^2(\mathbb{R})$ с нормой $\sqrt{n / \pi}$. Как видно, при росте $n$, норма тоже растет неограниченно, а значит $f_n$ расходится. Но что происходит с последовательностью скалярных произведений $\left< f_{n}, \phi \right>$, где $\phi \in L^{2}(\mathbb{R})$ — любая? Смотрим внимательно:

$lim_{n \to \infty} \int_{-\infty}^{\infty} f_{n}(x) \phi(x) dx = lim_{n \to \infty} \int_{-\infty}^{\infty} \frac{sin (nx)}{\pi x} \phi(x) dx = $

что равно

$= \phi(0) lim_{n \to \infty} \int_{-\infty}^{\infty} \frac{sin (nx)}{\pi x}dx + lim_{n \to \infty} \int_{-\infty}^{\infty} sin (nx) \frac{\phi(x) - \phi(0)}{\pi x} dx = \phi(0) lim_{n \to \infty} \int_{-\infty}^{\infty} \frac{sin (nx)}{\pi x}dx + \int_{-\infty}^{\infty} lim_{n \to \infty} sin (nx) \frac{\phi(x) - \phi(0)}{\pi x} dx$

Мы переставили местами предел и интеграл после избавления от неопределенности в $1/x$. Теперь, из ТФКП мы знаем (а если не знаем, то легко подсчитаем), что первый интеграл равен единице. Второй же стремится к нулю — это известное свойство интегралов с косинусами и синусами. Таким образом

$lim_{n \to \infty} \int_{-\infty}^{\infty} f_{n}(x) \phi(x) dx = \phi (0) = \int_{-\infty}^{\infty} \delta (x) \phi(x) dx$

$\delta(x)$ называется дельта-функцией и определяется просто как

$\int_{-\infty}^{\infty} \delta (x) f(x) dx = f(0)$

Разумеется, это не "обычная" функция, а функционал $\left<\delta,\cdot \right>$ на Гильбертовом пространстве, который берет функцию и возвращает её значение в нуле. Вполне можно написать $\delta(x-a)$, что соответствует значению функции в точке $a$ (это можно увидеть, подставив в интеграл $x' = x + a$).

Другое важное свойство дельта-функции: $f*\delta (x) = f(x)$, то есть свертка функции с дельтой дает эту же функцию. В этом плане многие функции образуют с дельта функцией так называемую сверточную алгебру, где дельта функция и свертка играют ту же роль, что и единица с операцией умножения для обычных чисел.

Возвращаясь к преобразованию Фурье, вспомним, что $F[\frac {sin(\omega_0 x)} {\pi x}](\xi)$ равно $1$ при $\left|\xi\right| < \omega_{0}$ и нулю иначе. При $\omega_{0} \to \infty$ образ становится равен просто единице, а его прообраз, соответственно, $\delta(x)$. Если вы хотите пропустить некий сигнал через такой фильтр, нужно свернуть этот сигнал с дельта функцией — и получить тот же сигнал на выходе, что является ожидаемым результатом (мы ведь фактически убрали ограничение по частоте, устремив $\omega_{0}$ к бесконечности).

Мой фильтр.

Подходим к самому интересному — тому, как я придумал свой фильтр. Не буду утверждать, что он не известен кому-либо ещё, просто я о нём точно не знал. Да и дизайн таких фильтров часто сводится к подбору так называемой оконной функции, у которой компактный носитель и на которую умножается идеальный фильтр. Я же пойду своим путём ;) Вспомним формулу дискретной свёртки:

$f_{n} = \sum_{i=-\infty}^{\infty} \phi_{i} \psi_{n-i}$

$\left\{ \phi_{i} \right\}$ здесь — ядро нашего фильтра, а $\left\{ \psi_{i} \right\}$ — сигнал. Пусть $\phi_{a} = \phi_{-a}$.

Для частотного анализа дискретных фильтров применяется так называемое Z-преобразование, которое тоже похоже на преобразование Фурье (и Лапласа). Но узнал я о его существовании несколько позже. А сначала я написал этот дискретный фильтр как непрерывный, используя с некоторой натяжкой дельта-функцию:

$\phi(t) = \sum_{n = -N}^{N}\phi_{n} \delta (t + n \frac {2 \pi}{\omega_{ref}})$

$\omega_{ref}$ — как раз наша частота дискретизации (угловая).

Применяя свойство сдвига (2), линейное свойство (1) и факт того, что $F\delta(t) = 1$ получаем Фурье-образ функции $\phi(t)$:

$\Phi(\xi) = \sum_{n=-N}^{N} \phi_{n} e^{in \frac {2\pi}{\omega_{ref}} \xi}$

Помня, что $\phi_{n} = \phi_{-n}$ перепишем это в виде:

$\Phi(\xi) = \sum_{n=-N}^{N} \phi_{n} e^{in \frac {2\pi}{\omega_{ref}} \xi} = \phi_{0} + \sum_{n=1}^{N} \frac{\phi_{n}}{2} cos(n \frac {2\pi}{\omega_{ref}} \xi)$

Здесь мы скомбинировали положительные и отрицательные экспоненты в косинусы по формуле Эйлера. Стоит заметить, что $\Phi(\xi)$ вещественнозначна (при вещественном аргументе). Это очень хорошо, так как такой фильтр не будет иметь задержки сигнала при положительном значении $\Phi(\xi)$ (и задержку по фазе $\pi$ при отрицательном). Мы видим здесь, что $\Phi(\xi)$ состоит из суммы функций $1$ и $cos(n \frac {2\pi}{\omega_{ref}} \xi)$ с разными натуральными $n$. Эти функции составляют базис в подпространстве $L^{2}[-\omega_{ref}/2, \omega_{ref}/2]$ для четных функций. Отлично, так как наш идеальный фильтр (напомню, равный $1$ для $\left|\xi\right| < \omega_{0}$ и нулю иначе) — четная функция. Введем переменную $a \le 1$ так, что $\omega_{0} = a\omega_{ref}/2$. Мы можем разложить идеальный фильтр в ряд Фурье по косинусам, получая коэффициенты:

$\phi_{0} = \frac{2}{\omega_{ref}}\int_{0}^{a\omega_{ref}/2}d\xi = a$

$\phi_{n} = \frac{4}{\omega_{ref}}\int_{0}^{a\omega_{ref}/2} cos (n \frac{2\pi}{\omega_{ref}}\xi) d\xi = \frac{2}{n\pi}sin (a\pi n)$

Таким образом, получаем наш рецепт даунсемплинга:

1. Выбираем коэффициент $a$, на который мы хотим изменить частоту дискретизации. Для преобразования 96 кГц -> 48 кГц $a = 1/2$.
2. Считаем коэффициенты $\left\{ \phi_{n} \right\}$ по формуле выше.
3. Сворачиваем наш сигнал с последовательностью $\left\{\cdots, \phi_{2}/2, \phi_{1}/2, \phi_{0}, \phi_{1}/2, \phi_{2}/2, \cdots\right\}$
4. Из готовой последовательности берем каждый $1/a$-й семпл. Для 96 кГц -> 48 кГц — каждый второй.
5. Если $1/a$ не целое число (например, при преобразовании 96 кГц -> 44.1 кГц) в входной сигнал перед фильтрацией вставляют нулей по вкусу. Например, $a = m/n$ — рациональное. Между семплами вставляют $m-1$ нулей, фильтруют с $a = 1/n$ и берут каждый $n$-й семпл.

Такой фильтр имеет недостаток — около места разрыва идеального фильтра (при $\left|  \xi \right| = \omega_{0}$) в его разложении Фурье будет проявляться т.н. эффект Гиббса, заключающийся в безобразном поведении ;-) разложения в этом месте. Чтобы сгладить этот эффект я ввел некую зону перехода, в которой $\Phi(\xi)$ находится где-то между нулём и единицей.

Я решил найти функцию, которая отвечает свойствам:

• $f(x) = f(-x)$, т.е. является четной
• $f(x) \in C[0,1]$
• $f(0) = 1$ и $f(1) = 0$
• $f'(0) = 0$ и $f'(1) = 0$

Вот пример такой функции: $f(x) = x^{4} - 2x^{2} + 1$. Теперь "втиснув" её в зону перехода я получаю гладкую функцию. Вот картинка Фурье-образа $\Phi(\xi)$ моего фильтра и частичная сумма 30 членов разложения его в ряд Фурье для $a = 1/2$:

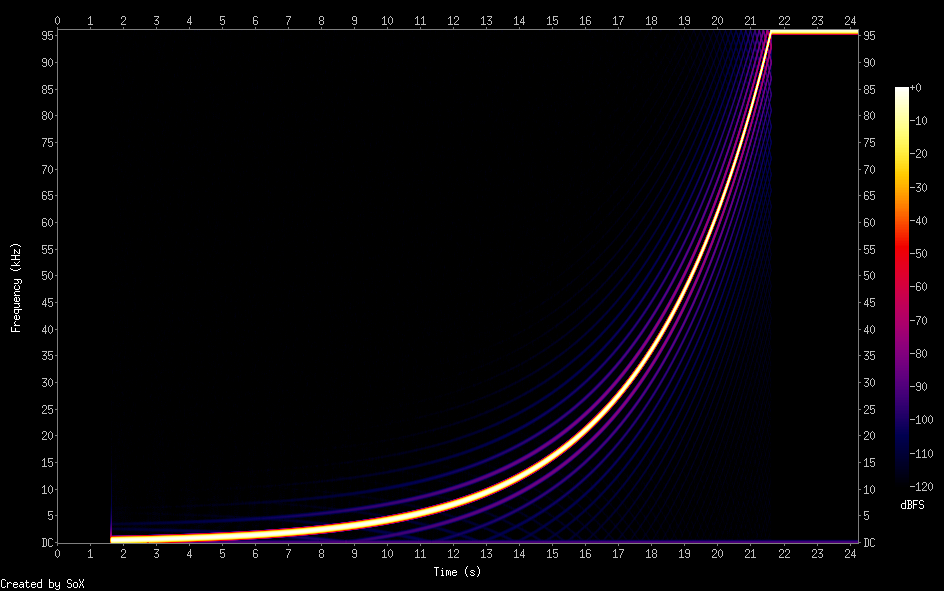
Управляя шириной переходной зоны и количеством членов в разложении можно получить весьма приемлемый результат. Например, возьмем входной сигнал с таким вот спектром:

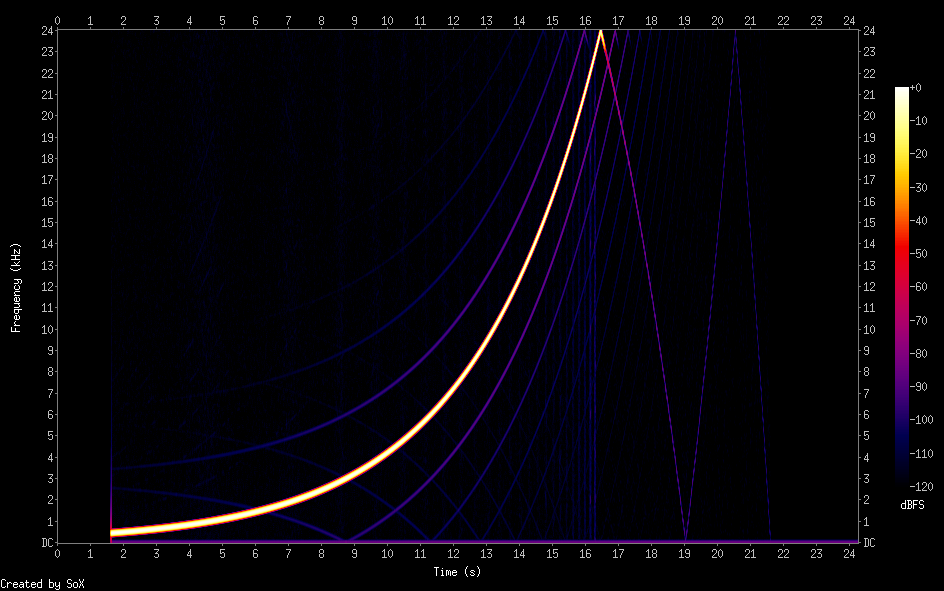
Здесь гармонические колебания нарастают по частоте до 96 кГц (частота дискретизации — 192 кГц). Применяем наш фильтр и даунсемплим до 48 кГц. Получаем следующий сигнал:

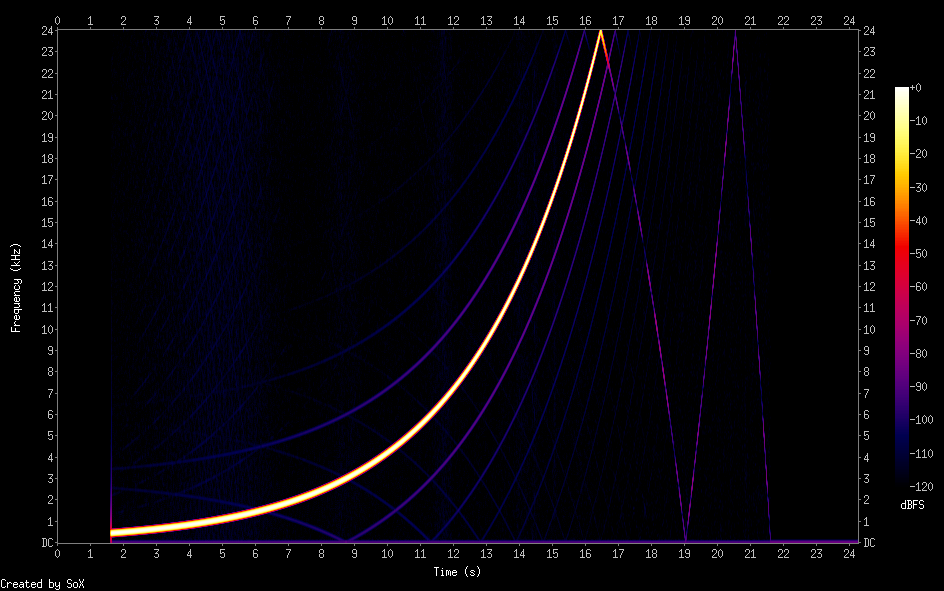
Как видно, весь сигнал выше 24 кГц не порезался, но заметно поубавился. Вот что выдает ffmpeg при стандартных настройках (команда ffmpeg -i input.wav -ar 48000 output.wav):

Ещё хуже. Зато soxr самый лучший ресамплер, тут побить его моей самоделке не представляется возможным. Да, стоит сказать, что имеет смысл сравнение при равном порядке фильтра. Тут на малых порядках (до 30-50) ffmpeg дает всё же лучший результат, а на больших лучше мой. При этом скорость работы весьма сносна.

Реализация всего этого добра на Common Lisp: https://github.com/shamazmazum/cl-audio-downsample