Очень занятная задачка в игре Sanitarium.

Sanitarium — невероятно интересный (по мнению автора) квест 1998 года выпуска про учёного-микробиолога по имени Макс, попавшего в сумасшедший дом после потери памяти в результате автомобильной аварии. По ходу игры Макс перемещается между параллельными мирами, придуманными силой воображения… Одним словом, лучше поиграть, а не читать спойлеры.

В части игры "Лаборатория" (7 часть) представлена очень интересная задача. Нужно открыть восемь круговых зацепов, охватывающих камень, чтобы тот упал. Зацепами управляет треугольная крестовина (на самом деле, 4-х угольная, но один конец там поломан и не влияет на зацепы) на пульте управления. Крестовину можно повернуть вокруг оси на одну позицию в любую сторону. При нажатии на кнопку, зацепы, соответствующие положению крестовины, меняют своё состояние (запертый зацеп отпирается, открытый — закрывается). Вот скриншот для ясности:

Цель оригинальной головоломки, как я сказал, — открыть все зацепы. Я предлагаю усложнённый вариант —

1. Найти все конфигурации крестовины, при которых решение (открытие всех зацепов) возможно и привести это решение.
2. Выполнить пункт 1 для произвольного количества зацепов.

Вот некоторые мои соображения:

Состояние зацепов и крестовины можно обозначать многочленами вида $\sum_{i=0}^{7} a_{i}x^{i}$, где $a_{i} \in \{0,1 \}$. Ноль обозначает закрытый зацеп, 1 — открытый. Положение и конфигурацию крестовины также обозначим многочленом, например $f(x) = x^4 + x^2 + 1$ обозначает положение крестовины как на картинке справа.

Введём операцию сложения на множестве коэффициентов многочленов как $c = a + b \mod 2$. На множестве многочленов операция сложения действует складывая коэффициенты при равных степенях, например $(x^4 + 1) + (x^4 + x) = x + 1$. Очевидно, что такая операция будет соответствовать нажатию на кнопку, меняющую состояние зацепов.

Эта операция обладает свойствами:

1. Ассоциативность: $(p_{1}(x) + p_{2}(x)) + p_{3}(x) = p_{1}(x) + (p_{2}(x) + p_{3}(x))$ в силу ассоциативности сложения на $\mathbb{Z}_{2}$.
2. Коммутативность: $p_{1}(x) + p_{2}(x) = p_{2}(x) + p_{1}(x)$ в силу того же.
3. Наличие нейтрального элемента: $p(x) + 0 = p(x)$.
4. Наличие обратного элемента: $p(x) + p(x) = 0$. (Каждый элемент — сам себе обратный)

Эти многочлены образуют коммутативную группу с операцией сложения.

Осталось ввести операцию, поворачивающую крестовину на одну позицию вправо (повороту влево будет соответствовать 7 поворотов вправо).

Будем искать её в виде $p'(x) = p(x)q(x) \mod c(x)$, где $p(x)$ — многочлен, соответствующий позиции крестовины. Очевидно, что $x \cdot x^{n-1} = x^{n}$ для $n = \overline{1,7}$, т.е $q(x) = x$ (по модулю $c(x)$) Так как $p'(x)$, остаток от деления на $c(x)$, может достигать седьмой степени, то $\deg c(x) \geq 8$ (не совсем очевидный факт, ну да ладно:). При повороте $x^7$ результат "заворачивается" и становится равным $1$, т.е. $x^8 \mod c(x) = 1$ или $x^8 - 1 = k(x)c(x)$. Так как $\deg (x^8-1) = 8 = \deg k(x) + \deg c(x)$ и $\deg c(x) \geq 8$, то получаем $\deg k(x) = 0$ и $\deg c(x) = 8$. Очевидно, что $k(x) = 1$ и $c(x) = x^8 + 1$ (помним, что $-1 = 1$).

Итак, ввожу вторую операцию — умножение многочленов по модулю $x^8 + 1$. Её свойства:

1. Ассоциативность: $x^{n}(x^{m}p(x)) = x^{n+m}p(x)$. Словами звучит так: поверни вправо 2 раза, а потом 3 раза — получишь поворот на 5 позиций.
2. Коммутативность: $p(x)q(x) = q(x)p(x)$.
3. Дистрибутивность: $p(x)(a(x) + b(x)) = p(x)a(x) + p(x)b(x)$. По сути это означает, что имея многочлен конфигурации крестовины $p(x)$ и многочлен $q(x)$ можно описать результирующее положение зацепов, полученное после последовательности поворотов и нажатий на кнопку.
4. Наличие нейтрального элемента: $1\cdot p(x) = p(x) \cdot 1 = p(x)$.

Множество наших многочленов степени вплоть до седьмой вместе с операциями сложения по модулю 2 и умножения по модулю $x^8 + 1$ образуют кольцо (но не поле!).

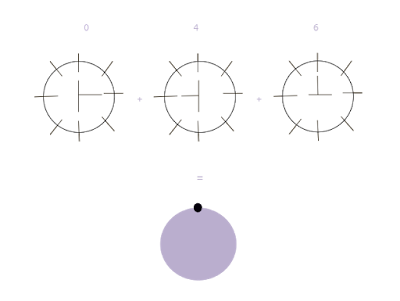
Приведу пример, какой с этого прок. В чём смысл произведения $(x^4 + x^2 + 1)(x^6 + x^4 + 1) = 1$? Смотри картинку:

Крестовину, описанную первым сомножителем мы повращали на 6, 4 и 0 позиций, сложили результат и получили ответ, что верхний зацеп будет открыт. Именно так, по одному зацепу, решается головоломка в игре.

Первый вопрос, поставленный в начале поста, таким образом, хотя бы частично сводится к отысканию многочленов $p(x)$, для которых существует обратный многочлен $q(x)$, т.е. $p(x)q(x) = 1$. Открыв первый зацеп, мы откроем их все, воспользовавшись свойствами умножения: $p(x)(q(x) + xq(x) + \cdots + x^{7}q(x)) = p(x)q(x)(1 + x + \cdots + x^{7}) = 1 + x + \cdots + x^7$. Как решить эту задачу пока не знаю, но думаю, рано или поздно узнаю ;) Единственная очевидная вещь, что существует тривиальное решение, когда крестовина описывается одночленом, т.е. $p(x) = x^n$ при $n = \overline{0,7}$

Да, ещё одно интересное наблюдение. Так как многочлен $x^8+1$ нетривиально разлагается на множители, т.е. $x^8 + 1 = (x+1)^8$, то с крестовиной, описываемой многочленом $k(x)(x+1)$, существуют нетривиальные манипуляции, которые не меняют состояние зацепов. Иными словами, существуют многочлены $p(x) \neq 0$, $q(x) \neq 0$, такие что $p(x)q(x) = 0$. Пример: проверить, существует ли многочлен $q(x) \neq 0$, такой что $(x^5 + x^4 + x + 1)q(x) = 0$? Замечаем, что $(x^5 + x^4 + x + 1) = (x + 1)(x^4 + 1)$. Ответ: да , $q(x) = x^4 + 1$. Смотрим картинку:

Ясно, что в силу симметрии достаточно повернуть такую крестовину не на 8 позиций, а всего лишь на 4, чтобы она отобразилась сама в себя.